Electronic Von Frey:
the facts

Can a force transducer replicate (or even improve) the measurements made by filaments?

This website discusses how von Frey filaments work, looks at their limitations and analyses the requirements for an electronic force transducer to replace them for mice.

There's a technical discussion below, so here's a quick summary:

The force range of the filaments used for mice usually runs from 0.07g to 6g, so the highest force applied is 6/.07 = 85 times the lowest one. But the filaments all have different diameters and mechanical nociceptive threshold is linearly related to diameter. This contracts the scale of "nociceptive stimulus" by a factor of nearly 3. So the 6g filament only applies 31 times as much stimulus as the 0.07g.

We should not therefore expect an electronic force transducer, with a probe of fixed diameter, to make measurements that can be compared directly with filaments. At 6g, the EvF really will apply 85 times as much nociceptive stimulus as at 0.07g. Measurements of both hypo and hyperalgesia, made with EvF, should therefore show smaller differences from baseline threshold than measurements made with filaments.

The force range required for mice is very small, and the conditions of the measurement (handheld, live animal etc) mean that simply attaching a probe to an existing commercial force transducer is not a great solution, especially if it has a force range much greater than required.

Topcat Metrology is a small bioscience company dedicated to the measurement of pain in all animal species. We make nociceptive threshold testing systems for most species from mice to camels and we've been doing it for twenty years. As part of that, we developed MouseMet, our own suite of integrated nociceptive tests for mice, including an Electronic von Frey, designed completely from first principles. It was our experience with filaments when doing this that prompted the construction of this website as an information resource. Most of it is also applicable to rats.

If you have experienced any of these issues, we'd like to hear from you particularly if you have some numbers you can share (in confidence).

Von Frey Filaments are very simple:

They are straight "springy" nylon rods of differing diameters (and slightly different lengths), supplied in sets. Each one buckles (elastically) at a force determined mainly by its diameter, but also influenced by its length. The nociceptive stimulus generated is not simple to analyse because, as they buckle, the contact area changes from a circle to something like a semi-circular line (depending on how much the tissue has deformed).

The force range of this set runs from 0.008gf to 300gf, so it's suitable for both mice and rats. To use, one would test first with a filament close to the expected threshold value (eg 2g). If the mouse responded, one would then test with the next filament down (1.4g). If it didn't respond, one would try the next filament up (2g) and so on until five changes in direction have been recorded. A mathematical algorithm called the up-down method is then used to derive the theoretical threshold.

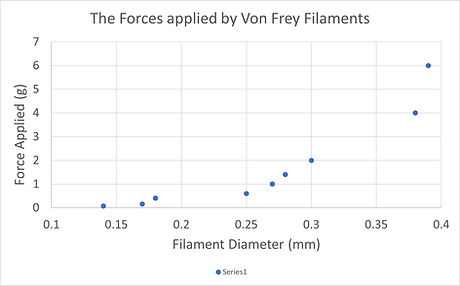
Here's a graph of the forces applied by a typical set of von Frey filaments, plotted against their diameter.

These are the filaments typically used in mouse testing: 0.07g -6g. If they were all the same length, this graph would be a smooth curve (as the buckling force of an elastic column is related to the third power of the diameter). But, as the manufacturer is constrained by the diameters of filament material available, the force progression required (for the up-down method) is arrived at by varying the length as well (because a longer filament buckles at a lower force than a short one of the same diameter). That's why the graph is "lumpy".

But the changing area of the filaments complicates the stimulus applied:

Pressure = Force/Area so you might expect that, if you doubled the diameter of a probe, you would need to apply four times the force to achieve the same nociceptive threshold.

This however is not so: it's well accepted that the increase in force required is linearly related to the DIAMETER of the probe, not its area.

So a 10mm probe will only require 5 times the force to achieve the same nociceptive threshold as the 2mm probe in the image above.

Click here for a paper demonstrating this.

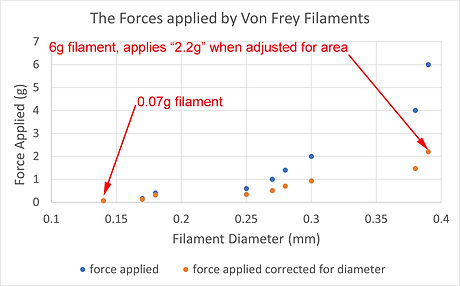
Here's the same graph (blue dots) but with the force values "adjusted" for the increase in diameter of the higher force filaments (orange dots).

The correction has been made relative to the smallest one in the series (0.07g). It doesn't matter where you choose your base line point, you'd get the same effect but with different numbers. So its important to remember that the scale for the orange dots is no longer an absolute force scale, it's a "nociceptive stimulus scale". The important point is that the 6g filament only applies 31 (2.2/0.07) times as much nociceptive force as the 0.07g filament, not 86 (6/0.07) times as much.

$filaments weber fraction.jpg$

Also...the Weber Fraction of a filament set varies considerably:

What's that??

Animals (including humans) don't notice very small changes in the level of a stimulus. The smallest increment, expressed as a ratio, is known as The Weber Fraction. So if a human, for instance, can detect 10N with a particular probe and can then just detect 15N as being "a bit more force" then the Weber fraction would be 15/10 = 1.5. As it's a constant ratio, the next increment they would theoretically be able to detect would be 15 *1.5 = 22.5N. And so on.

These increments, 10N, 15N and 22.5N are therefore a scale of convenient testing points (for this particular case) to detect differences. Which is what filaments do.

The up-down method recommends that the Weber fraction is about equal to the standard deviation of the data (so you sort of need to know the answer before you start) but that it can vary up and down by up to 50%. But as you can see from this graph, the effective Weber fraction of the filaments varies a lot more than that. In particular, there's barely any difference in nociceptive stimulus between the 0.4 and 0.6g filaments (because the filament diameter has changed so much).

This is another reason why filaments may give a different answer to EvF; the filament scale is quite distorted in some parts of its range. On the other hand, filaments are probably better at applying the very small forces (<0.5g).

Electronic Von Frey:the facts